Problem is Shared Memory
For these intructions in two cores:
| Core C1 | Core C2 | * |
|---|---|---|
| S1: x = 1 | S2: y = 1 | x and y initialy be 0 |
| L1: r1 = y | L2: r2 = x |
We could get different results depending on the order of execution:
| r1 | r2 | Execution Order |
|---|---|---|
| 0 | 1 | S1 L1 S2 L2 |
| 1 | 0 | S2 L2 S1 L1 |
| 1 | 1 | S1 S2 L1 L2 |
| 0 | 0 | *Possibly when using FIFO write buffers. |
Consistency vs Coherence?
- Cache coherence does not equal memory consistency. Coherence simply provide a pipelined way to update the cache. It along does not determine shared memory behavior.
- A memory consistency implementation can use cache coherence as a useful “black box.”
Sequential Consistency (SC)
Most intuitive memory model. Basic idea:
- Single processor sequential: result like executed in order.
- Multi-processor sequential: single core in the sequence of in order, while all core also execute in some sequential order. The total order of operations is
memory order, like this figure:
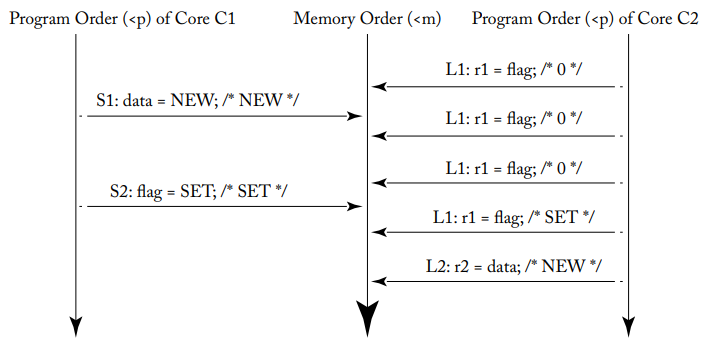
Here is a example SC execution for the preious sample table of execution S1 S2 L1 L2.
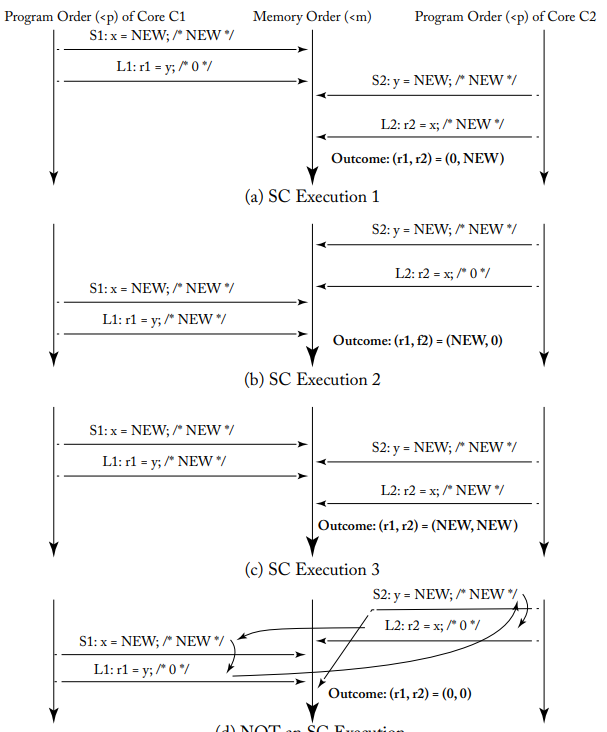
SC Execution
Reqires the following (L(a) and S(a) represent a load and a store, respectively, to address a, Orders <p and <m define program and global memory order.):
- All cores insert request to <m respecting to their programe order. Four cases:
- If L(a) <p L(b) -> L(a) <m L(b) /* Load->Load */
- If L(a) <p S(b) -> L(a) <m S(b) /* Load->Store */
- If S(a) <p S(b) -> S(a) <m S(b) /* Store->Store */
- If S(a) <p L(b) -> S(a) <m L(b) /* Store->Load */
- Every load gets the value from the latest store in memory order.
SC implementation
2 Native implementation:
- Multistasking Uniprocessor
- Multi threading in single processor.
- T1 executes on C1 until context switch to T2
- On a context switch, all pending memory requests must complete before switching.
- Multi threading in single processor.
- Switch
- Pick a core, complete one request, and then switch to next core.
- Can be random, round-robin, or any other scheme that does not starve a core.
SC Implementation with Cache Coherence
Conflict: two operations to the same address in parallel, and at least one writes.
Here assume SWMR(Single Writer Multi Reader)
State Machine:
- M: modified - read and write permit
- S: shared - read permit
- GetM and GetS: coherence requests to obtain a block in M or S.
- Requests can perform in parallel is no conflict.
Optimizing SC Implementation
- Non-Binding Prefetching
- Speculative Cores: When branch prediction squashes intructions, the non-binding prefetching does not get squashed.
- Dynamically Scheduled Cores: out-of-order execution.
- Multithreading
Atomic operations with SC
Atomically perform paris of operations for thread synchronization. Read-Modify-Write (RMW) aka:
- Load-Linked/Store-Conditional (LL/SC)
- Test-and-Set (TS)
- Compare-and-Swap (CAS)
- Fetch-and-Add (FAA)
RMW atomically read to check if it is unlocked, and write the locked value. To be atomic, read and write must appear consecutively.
Atomic RMW does not need to inform other cores.
- The core obtain the block in M in its cache.
- If block is not M or not there, just load and store the block in its cache.
- Serve any incoming coherence requests intil it stores.
TSO/X86
Motivation
write buffer hold the committed store until it retire and write to cache/register. More performance improvement can be done by forward/bypass the latest store to load.
Back to the example:
| Core C1 | Core C2 | * |
|---|---|---|
| S1: x = 1 | S2: y = 1 | x and y initialy be 0 |
| L1: r1 = y | L2: r2 = x |
- C1 run S1, and buffer NEW to write buffer
- C2 run S2, and buffer NEW to write buffer
- Both run L1 and L2, which both get 0 from memory
- Finally both write buffers update x and y to NEW
TSO compare to SC
SC execution is a subset of TSO execution.
Store->Load in program order not necessary be the same in memory order, so SC has this but TSO does not:
- If S(a) <p L(b) -> S(a) <m L(b) /* Store->Load */
Programmer/Compiler can prevent this by using FENCE instruction. Memory operation before FENCE must complete before any memory operation after FENCE.
Bypassing
Most bypassing value can only be within its own thread.
Atomic
Load of RMW cannot pass an earlier store because of this wrong scenario:
- Load of RMW pass earlier store.
- Store of RMW pass earlier store because they are atomic pare.
- Store passing store is illegal in TSO.
To fix this:
- RMW effectively drains/runs the write buffer before it can perform the load.
- Load part need read-write coherence permission.
- Cannot change/relinquish permission in the middle of RMW.
Relaxed Memory Consistency
- Can reorder any memory operation unless there is a FENCE.
- Requires programmer to explicitly mark the FENCE.
Some advantages:
- Non-FIFO Coalescing Write Buffer
- Simpler Implementation
- Coupling consistency and coherence: Relaxed Model opens the coherence box.
eXample relaxed Consistency model (XC)
XC gratrnteed to preserve program order for:
- Load/Store -> FENCE
- FENCE -> FENCE
- FENCE -> Load/Store
XC keeps TSO rules for two same address access:
- Load -> Load/Store
- Store -> Store
For example for this case, we have to insert FENCE at these places to get r2 = 1:
| Core C1 | Core C2 | * |
|---|---|---|
| S1: x = 1 | ||
| F1: FENCE | ||
| S2: y = 1 | ||
| L1: r1 = x | ||
| B1: if (r1≠ 1) goto L1; | ||
| F2: FENCE | ||
| L2: r2 = y |
Implementation
- Each core has a Reorder Buffer (ROB) to reorder load and store.
- Reorder based on RC rules.
- FENCE:
- FENCH as drain: costly but common.
- FENCH as no-ops: not in commercial product yet.
Atomic
The same as TSO: drain the write buffer before performing RMW. However, XC needs a FENCH for RMW or lock release.
For examples:
| Note | XC Inst |
|---|---|
| Read L and hold L if L is 0 | RMW: L If L==1, goto RMW; FENCE |
| Critical Sections | Memory Requests |
| Release Lock | FENCE; Store L=0 |
Data Races
Assume acquire lock and release lock always has FENCH to perform the correct mutual exclusion.
In this case, r1 and r2 can be any combination of 0 and 1. There is a data race.
| Core C1 | Core C2 | * |
|---|---|---|
| lock | ||
| S1: x = 1 | L1: r1 = y | x and y initialy be 0 |
| S2: y = 1 | L2: r2 = x | |
| unlock |
Now, r1 and r2 can only be (0,0) or (1,1). There is no data race.
| Core C1 | Core C2 | * |
|---|---|---|
| lock | lock | |
| S1: x = 1 | L1: r1 = y | x and y initialy be 0 |
| S2: y = 1 | L2: r2 = x | |
| unlock | unlock |
References
Sorin, D. J., Hill, M. D., Wood, D. A., & Nagarajan, V. (2020). A primer on memory consistency and cache coherence (2nd ed., pp. 17-90). Springer Nature. https://doi.org/10.1007/978-3-031-01764-3